Episodes of George Shiber's Lectures
Mark All
A proof: if every uncountable model of a theory T is omega-saturated and T is superstable, then T is categorical.
Exploring liberational theories of oppression under the principle of ontological pluralism
Model-completion, ultrapower-saturation and intra-theoretic rationality in mathematical practice
A short reply to a 4-Dimensionalist attack against 3-dimensionalism
A universalistic/virtue ethic critique of Fletcher's basic contention that loyalty is the central and ineliminable feature of morality.
A modal-essentialist solution to Chrysippus' puzzle.
A critical appraisal of Susy and String Theory: a devil's advocate's perspective
Some remarks on mathematics and quantum field theory, part 1.
Strongly compact cardinals, elementary embeddings and characterization by fixed points and fine ultrafilters.
Two versions of Curry's paradox are presented, a paradox highly regarded as the most vexing and the most threatening to a consistent and viable truth-theory, with some conclusions drawn.
Kant on Human Spontaneity, Autonomy, the Natural Order and the Moral Order
On the Principles Of Possible Action and Of Prevention.
Short of provable inconsistency, what are the strongest large cardinal axioms, and a look at extending into inconsistency with paraconsistent dialethicist truth-theory
on the illusion of first-person knowledge of intentional states and reflections what could count as neuropsychological evidence of consciousness
On the provability or non-provability of certain mathematical theorems wiithin 'weak' subsystems of second-order number theory in relation to differential equations, in particular, the Cauchy-Peano existence-theorem for solutions to differentia
I construct a model in which 'strongness' of a cardinal k is indestructible under k+-weakly closed Prikry Forcing, and a solution to Hajnal's Conjecture
On the problem of shared preferences of 2 or more Bayesian decision makers and the necessity to indexicalize conditionalization, and some reflections on the impact on theory-selection in science
Democratic vs. Political Egalitarianism: two critiques and a look forward
Some of my proofs that superstring (M) Theory is the only possible GuTheory, and some reflections on the philosophy of physics/science (the 'physical' proofs will be provided in pdf-form and linked in various groups and my page)
In defense of DE and the principle of luck-equality and reciprocity
on supersymmetric gauge invariance and the uniqueness of superstring-M-Theory w.r.t. gauge/gravity dualities and shrodinger symmetries (lecture 3, part 2)
On what do aestheic pleonastic evaluations and 'properties' supervene
Reflections on the relative consistency of large cardinals in the range between supercompact to Vopenka's Principle, and the limits of large cardinal axioms
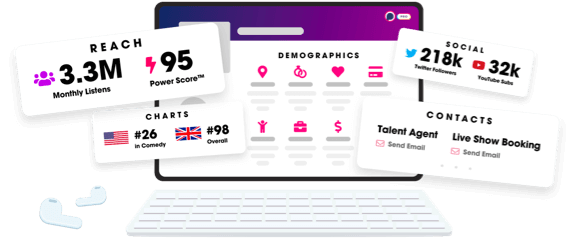
Unlock more with Podchaser Pro
- Audience Insights
- Contact Information
- Demographics
- Charts
- Sponsor History
- and More!
- Account
- Register
- Log In
- Find Friends
- Resources
- Help Center
- Blog
- API
Podchaser is the ultimate destination for podcast data, search, and discovery. Learn More
- © 2025 Podchaser, Inc.
- Privacy Policy
- Terms of Service
- Contact Us
