Like addition and multiplication on Church-encoded numbers, exponentiation can be assigned a type in simply typed lambda calculus (STLC). But surprisingly, the type is non-uniform. If we abbreviate (A -> A) -> A -> A as Nat_A, then exponentiation, which is defined as \ x . \ y . y x, can be assigned type Nat_A -> Nat_(A -> A) -> Nat_A. The second argument needs to have type at strictly higher order than the first argument. This has the fascinating consequence that we cannot define self-exponentiation, \ x . exp x x. That term would reduce to \ x . x x, which is provably not typable in STLC.
Show More
Unlock more with Podchaser Pro
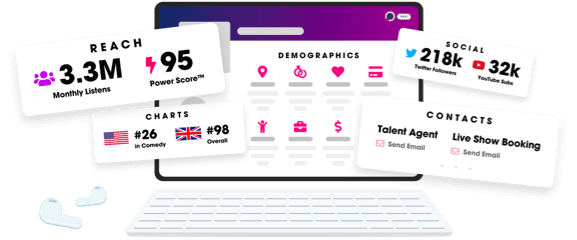
- Audience Insights
- Contact Information
- Demographics
- Charts
- Sponsor History
- and More!
- Account
- Register
- Log In
- Find Friends
- Resources
- Help Center
- Blog
- API
Podchaser is the ultimate destination for podcast data, search, and discovery. Learn More
- © 2025 Podchaser, Inc.
- Privacy Policy
- Terms of Service
- Contact Us
