My Favorite Theorem
A Science podcast
Episodes of My Favorite Theorem
Mark All
Jeremy Alm likes the Rado graph, a weird object that captures all sorts of interesting properties of finite graphs. Also cheese.
Robin Wilson likes the Hopf Index Theorem and we agree. Also, hot fudge.
Kate Stange is a number theorist who loves quadratic forms (and who doesn't, really). Her favorite theorem is the bijection between them and ideal classes. Also chocolate.
Karen Saxe is an analyst who spends her days representing mathematics on Capitol Hill. She really likes the isoperimetric inequality and its many uses. Also tennis.
Corrine Yap loves math, graph theory in particular, and also loves to perform her one-person play about Sonya Kovalevskaya. Also, tofu.
Allison Henrich studies knots and her favorite theorem is about how one might unknot a knot. Also, music.
We all know the (probably apocryphal) story of Gauss adding up the first 100 positive integers as a child. Well, Tom Edgar really likes this result and will be happy to tell you about dozens of different ways to prove it. Also, Groundhog Day.
Tatiana Toro is a geometer and therefore loves the ur-theorem of geometry, "due" to Pythagoras. She also likes to walk.
Gresham Professor of Geometry Sarah Hart likes cycloids and we talk at length about all their fascinating properties. Also, Moby Dick (or The Whale).
Euler's polyhedral formula continues to amaze Matthew Kahle as he finds it showing up in different places in mathematics. Also, Bach.
Kevin visited Texas Christian University in March and recorded this episode with some math students. Excellent theorems and pairings.
Cihan Bahran has a popular twitter feed in which he shares surprising theorems. His favorite? Matrix mortality is undecidable.
Juliette Bruce is an algebraic geometer who loves to think about embedding curves in projective space. Also mountaineering.
Technically this is a theorem, but it seems so obvious that it's unclear that it needs a proof. In this episode Christopher Danielson points out that polygons have same number of sides as vertices. Many shapes make an appearance.
Kimberly Ayers likes dynamics and so obvs her fave theorem is Sharkovskii's result that "period 3 implies chaos." Also taffy.
Philip Ording wrote a cool book (you should check it out) and he likes the Erlangen Program. Not really a theorem, but we're not purists around here.
Daina Taimina is famous for her adventures in mathematical crocheting, but her favorite theorem comes from Desargues. She also likes to travel.
Tien Chih loves combinatorics, which means he really loves proving things by induction. In this episode we have a good time learning about this incredibly useful technique in mathematics.
We are joined by a group of math students at Cal State University in Los Angeles for a diverse collection of theorems and pairings.
We can't believe it took 75 episodes to get to the Banach-Tarski paradox, but finally Dave Kung chose it as his favorite theorem. Also, Enigma Variations.
An old favorite theorem makes its third appearance on the pod, but we always like to learn new points of view. Priyam Patel likes the Brouwer Fixed Point theorem, and this time we learn how it helps classify isometries of hyperbolic space. Also
Courtney Gibbons likes isomorphism theorems. All three of them, in fact, and she wants to remind you they are due to Emmy Noether, despite most textbooks ignoring that fact. Also, bunnies.
Kameryn Williams is a logician and their favorite theorem is the less well-known Condensation Lemma of Gödel. Also brie.
Composer Emily Howard uses mathematical objects and ideas as inspiration for her orchestral and chamber pieces. In this episode we talk to her about "Torus" which was inspired by work with dynamicists.
Mathematician and philosopher Joel David Hamkins likes games (whatever those are) and his favorite theorem is that winning strategies exist. This requires defining "games", "strategies", and all kinds of other stuff. Also chess.
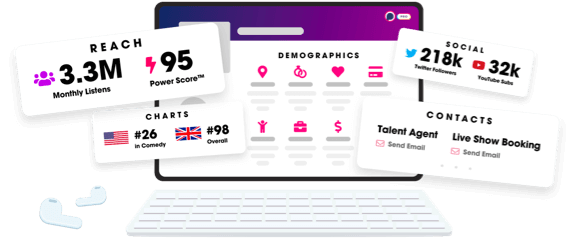
Unlock more with Podchaser Pro
- Audience Insights
- Contact Information
- Demographics
- Charts
- Sponsor History
- and More!
- Account
- Register
- Log In
- Find Friends
- Resources
- Help Center
- Blog
- API
Podchaser is the ultimate destination for podcast data, search, and discovery. Learn More
- © 2025 Podchaser, Inc.
- Privacy Policy
- Terms of Service
- Contact Us
